Polynomial basics

- post 1: Polynomial Basics
- post 2: Polynomials Ring
- approximation of more complex functions
- interpolation
- error correction codes
- graphical interpolation of curves (splines)
the structure
a polynomial is completely defined by a vector of values in a ring. These represents the polynomial coefficient from the lowest to the highest grade (let's call it  ); the highest grade coeddicient is supposed to be different from the zero of the ring, and all coefficient of degree greather than
); the highest grade coeddicient is supposed to be different from the zero of the ring, and all coefficient of degree greather than  are supposed to be zero.
Main operation needed to define a polynomial are sum and multiplication thus it can be possible to use rings different from usual built-in types (integer and floating point numbers) as long as multiplication and sum are defined.
Thus the data structure will contain a vector of values where sum and multiplication are defined. The vector is needed because we cannot know the length of the coefficient string in advance.
At first I will add only a public constructor: coefficients should be immutable from the user perspective.
I can also add a test to this file in order to make sure it is compiled properly. I will import Write in order to use a print debug and check all is ok
are supposed to be zero.
Main operation needed to define a polynomial are sum and multiplication thus it can be possible to use rings different from usual built-in types (integer and floating point numbers) as long as multiplication and sum are defined.
Thus the data structure will contain a vector of values where sum and multiplication are defined. The vector is needed because we cannot know the length of the coefficient string in advance.
At first I will add only a public constructor: coefficients should be immutable from the user perspective.
I can also add a test to this file in order to make sure it is compiled properly. I will import Write in order to use a print debug and check all is ok
#[derive(Debug)] pub struct Poly <T>{ coeff : Vec<T> } impl<T> Poly<T>{ pub fn new(coeff : Vec<T>) -> Poly<T>{ Poly{ coeff:coeff } } }
#[cfg(test)] mod tests { use super::Poly; #[test] fn creation_and_debug() { let x = Poly::new(vec![1,2,3]); assert_eq!(format!("{:?}", x), "Poly { coeff: [1, 2, 3] }"); } }
the basic operations
I'd like to evaluate a polynomial in a point of its coefficients' ring. In order to do that I need to use the following properties:
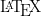 . By implementing the
let's check if the current implementation works
#+name poly1-test-display
. By implementing the
let's check if the current implementation works
#+name poly1-test-display
- sum is defined
- multiplication is defined
- there is a zero (neutral element of the sum)
- the ring values can be copied (i.e. there is a way to safely copy their binary representation)
Display trait it would be easier to use the format functions later.
use std::ops::{Mul, Add}; use std::fmt; #[derive(Debug)] pub struct Poly <T>{ coeff : Vec<T> } // I need to guarantee that a type has a neutral element for sum pub trait Zero{ fn zero() -> Self; } impl<T: Mul<Output = T> + Add<Output = T> + Copy + Zero> Poly<T>{ pub fn new(coeff : Vec<T>) -> Poly<T>{ Poly{ coeff:coeff } } pub fn eval(self : &Poly<T>, x : T) -> T { self.coeff.iter() .rev() .fold(T::zero(), |acc, c| acc * x + *c) } } impl<T: fmt::Debug> fmt::Display for Poly<T> { fn fmt(&self, f: &mut fmt::Formatter<'_>) -> fmt::Result { let result : Vec<String> = self.coeff.iter() .enumerate() .map(|(i, c)| format!("({:?})x^{}",c,i)) .collect(); write!(f, "{}", result.join(" + ")) } } // here are a couple of implementation of general use impl Zero for u32{ fn zero() -> u32 { 0 } } impl Zero for i32{ fn zero() -> i32 { 0 } } impl Zero for f32{ fn zero() -> f32 { 0.0 } }
#[test] fn test_evaluation() { let p = Poly::new(vec![1,2,3]); assert_eq!(p.eval(10), 321); } #[test] fn test_formatting() { let x = Poly::new(vec![1,2,3]); assert_eq!(format!("{}", x), "(1)x^0 + (2)x^1 + (3)x^2"); }
a polynomial can be a function too
Current implementations of rust expose some traits to pass functions and lambdas as objects in the
The following code creates the needed trait implementations. It can be compiled with
now we can call the polynomial directly as a function. let's add a few test also here:
std::ops module:
Fnwhen the data structure is borrowed without mutabilityFnMutwhen the data structure is borrowed with mutabilityFnOnewhen the ownership is transferred to the data structure
#![feature(unboxed_closures)] #![feature(fn_traits)]
cargo +nightly build
use std::ops::{Fn,FnOnce,FnMut}; impl<T: Mul<Output = T> + Add<Output = T> + Copy + Zero> Fn<(T, )> for Poly<T> { extern "rust-call" fn call(&self, args: (T,)) -> T { self.eval(args.0) } } impl<T: Mul<Output = T> + Add<Output = T> + Copy + Zero> FnMut<(T, )> for Poly<T> { extern "rust-call" fn call_mut(&mut self, args: (T,)) -> T { self.call(args) } } impl<T: Mul<Output = T> + Add<Output = T> + Copy + Zero> FnOnce<(T, )> for Poly<T> { type Output = T; extern "rust-call" fn call_once(self, args: (T,)) -> T { self.call(args) } }
#[test] fn test_call() { let p = Poly::new(vec![1,2,3]); assert_eq!(p(10), 321); }
let's see how it looks like
I'm going to plot a few polynomials using the popular
 This code was used to create the post initial image.
It uses the famous Taylor series expansion of the
This code was used to create the post initial image.
It uses the famous Taylor series expansion of the
plotters library.
use plotters::prelude::*; use poly::poly2::*; fn main() -> Result<(), Box<dyn std::error::Error>> { //polynomial definition let p0 = Poly::new(vec![0.0, 2.0, 0.0, -3.0]); //start of the plot let root = BitMapBackend::new("post002_plot0.png", (640, 480)).into_drawing_area(); root.fill(&WHITE)?; //the polynomial is formatted in the caption let mut chart = ChartBuilder::on(&root) .caption(format!("y={}",p0), ("sans-serif", 25).into_font()) .margin(5) .x_label_area_size(30) .y_label_area_size(30) .build_cartesian_2d(-1f32..1f32, -1f32..1f32)?; chart.configure_mesh().draw()?; //here the polynomial is evaluated //the polynomial is formatted in the plot label chart .draw_series(LineSeries::new( (-50..=50).map(|x| x as f32 / 50.0).map(|x| (x, p0(x))), &RED, ))? .label(format!("y = {}",p0)) .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &RED)); chart .configure_series_labels() .background_style(&WHITE.mix(0.8)) .border_style(&BLACK) .draw()?; Ok(()) }

sin
use plotters::prelude::*; use poly::poly2::*; // this evaluates the factorial of n fn fac(n : i32) -> i32{ let mut result = 1; for i in 1..=n{ result = result * i } result } fn main() -> Result<(), Box<dyn std::error::Error>> { //start of the plot let root = BitMapBackend::new("post002_plot1.png", (640, 480)).into_drawing_area(); root.fill(&WHITE)?; //the polynomial is formatted in the caption let mut chart = ChartBuilder::on(&root) .caption("Approximations of sin", ("sans-serif", 25).into_font()) .margin(5) .x_label_area_size(30) .y_label_area_size(30) .build_cartesian_2d(-7f32..7f32, -1.2f32..1.2f32)?; chart.configure_mesh().draw()?; //here the polynomial is evaluated //the polynomial is formatted in the plot label for (deg,color) in [(1,RED),(3,BLUE),(5,MAGENTA),(7,GREEN),(9,CYAN)].iter(){ let coeff : Vec<f32> = (0..=*deg) .map(|n| if n % 2 == 0 { 0.0 } else { let nf = fac(n) as f32; let sign = if ((n - 1) / 2) % 2 == 0 { 1.0 } else { -1.0 } ; sign/nf }) .collect(); let p0 = Poly::new(coeff); chart .draw_series(LineSeries::new( (-50..=50).map(|x| x as f32 * 7.0 / 50.0).map(|x| (x, p0(x))), &color, ))? .label(format!("sin{}",deg)) .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &color.clone())); } chart .draw_series(LineSeries::new( (-50..=50).map(|x| x as f32 * 7.0 / 50.0).map(|x| (x, x.sin())), &BLACK, ))? .label("sin") .legend(|(x, y)| PathElement::new(vec![(x, y), (x + 20, y)], &BLACK)); chart .configure_series_labels() .background_style(&WHITE.mix(0.8)) .border_style(&BLACK) .draw()?; Ok(()) }
conclusions
Polynomials are simple yet powerful structures which can dig into a language syntax and features.
This is just the beginning of this journey: stay tuned for more.

